このブログでは、「どんな企業に投資したらいいのか?」という具体的な話を中心にしていきたいと思いますが、投資を始める前にどうしても押さえておいてポイントが3つあります。
- 期待値を常に意識する
- 投資は原理的に儲かる仕組み
- 株は事業の一部
今日は「1.期待値を常に意識する」について書きます。
「期待値?数学の授業で習ったような・・・。でもこのブログって投資の話をするんじゃないの?」
・・・ええ、確かに数学の話です。
が、全ての投資判断に影響を与える重要な考えなので、まず一番に説明します。
全ての投資家は、期待値を強く意識しながら投資をしています。
なぜなら、投資というものは、短期的には運の要素により得をしたり損をしたりすることがあっても、長期的な結果は期待値に近づいていくからです。
期待値と期待収益率
期待値
「期待値」とは、「投じた金額に対して返ってくる見込みの金額」のことです。
要は、金がいくらになって返ってくるか、の目安です。
例えば、以下のようなゲームについて考えてみましょう。
お金を賭けてコインを投げる。
表が出たら賭け金の3倍が返ってくる。
裏が出たら賭け金は返って来ない。
※コインに細工はなく、表が出る確率も、裏が出る確率も1/2とする。
<ゲームA>に100万円を賭けた場合、得られる金額の期待値はいくらになるでしょうか。
中学の数学で習っているはずですが、念のためおさらいしておきましょう。
表が出れば、賭け金100万円の3倍、300万円が返ってきます。裏が出れば0円です。
表が出る確率も、裏が出る確率も1/2なので、期待値は以下の式で求められます。
300万円×1/2+0円×1/2=150万円
つまり、「<ゲームA>に100万円を賭けたら、だいたい150万円になって返ってくるだろう」ということです。
期待収益率
期待収益率という言葉も投資の話をする際によく出てきます。
「期待収益率」とは、「投じた金額に対して返ってくる見込みの金額の割合」のことです。
要は、金が何倍になって返ってくるか、の目安ということです。
「期待リターン」と言うこともあります。
<ゲームA>の期待収益率はいくらになるでしょうか。
期待値の計算では、投じた金額である100万円に対し、返ってくる見込みの金額(期待値)が150万円でした。
したがって、期待収益率は以下の式で求められます。
しかし、<ゲームA>で「1/2の確率で3倍、1/2の確率で0倍になる」というのは、投じた金額に関わらず一定なので、以下のように計算した方が簡潔です。
3倍×1/2+0倍×1/2=1.5倍=150%=+50%
つまり、「<ゲームA>に賭けたら、だいたい1.5倍になって返ってくるだろう」、または「賭け金の50%の利益が望めるだろう」ということです。
繰り返すほど結果は期待値に近づく
例えば、以下のような思考実験をしてみましょう。
あなたの全財産は100万円とします。
1人が複数会場にエントリーしても構いませんが、総額で100万円以上は賭けられません。
あなたならどのように賭けますか?例えば、以下の場合について結果を見てみましょう。
① 100万円全額を1会場で賭ける。
② 10万円ずつ10会場に分けて賭ける。
③ 1万円ずつ100会場に分けて賭ける。
④ 1000円ずつ1000会場に分けて賭ける。
① 100万円全額を1会場で賭けた場合
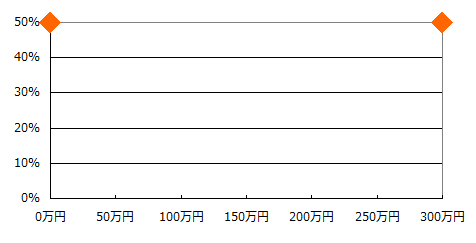
結果をグラフで表します。
横軸に得られる金額を、縦軸に確率を表しています。
50%の確率で300万円がもらえ、50%の確率で賭け金がパーになります。
さすがにこんな賭け方はリスクが大きすぎますね。
いくら期待収益率がプラスの賭けとはいえ、半分の確率で全財産を失うのですから。
② 10万円ずつ10会場に分けて賭けた場合
得られる金額は、17.2%の確率で0~90万円、65.6%の確率で120~180万円、17.2%の確率で210~300万円となります。
2割近い確率で100万円以上得するのは魅力的な反面、2割近い確率で10万以上損をするなら、まだちょっと怖いですね・・・。
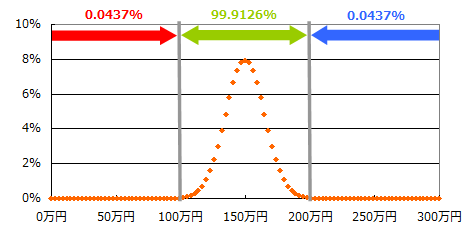
③ 1万円ずつ100会場に分けて賭けた場合
得られる金額は、0.0437%の確率で0~100万円、99.9126%の確率で100~200万円、0.0437%の確率で200~300万円となります。
0.0437%ということは2228回に1回ということです。それだけ低い確率でしか損しないなら、やりたい気がしますね。
もちろん大勝ちする確率も低いわけですが、一方で、10万円以上得する(得られる金額が110~300万となる)確率は99.398%です。
これだけ高い確率で10万円以上得するなら「まず勝てる賭け」と言えそうです。
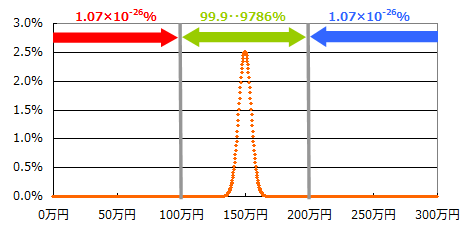
④ 1000円ずつ1000会場に分けて賭けた場合
得られる金額は、1.07×10-26%の確率で0~100万円、
99.9999999999999999999999999786%の確率で100~200万円、
1.07×10-26%の確率で200~300万円となります。
要は、得られる金額はほぼ確実に100~200万円になるってことです。
さらに言えば、30万円以上得する(得られる金額が130~300万となる)確率は99.9832%となります。
私だったら、この方法で賭けます。大勝ちする可能性は低いですが、確実な勝ちを取りに行きます。
大数の法則
①~④の賭け方を見ていくと、賭け金を分散するほど、得られる金額は期待値である150万円に近づく、ということがわかると思います。
これは「試行を繰り返すことで、結果は期待値に近づく」という確率が持つ性質のためです(「試行」とは<ゲームA>のような偶然の要素を伴う実験のことです)。
この性質を「大数の法則」と呼びます。
・・・でも、こんなもっともらしく説明されなくたってわかりますよね。
「コインを10回投げたら、表が8回、裏が2回のように偏りが生じることもあるが、さすがに1000回投げたら、だいたい表が出る回数は500回前後に落ち着くだろう」というのは直観的にわかります。
投資家にとっての期待値
確率論で言う「試行を繰り返す」は、投資では「分散」と「継続」にあたります。
分散:上記の思考実験で見られたように、分散をすればするほど、結果は期待値に近づきます。投資でも同じで、個々の投資対象のリターンは投資時に見込んだ期待収益率を大きく上回ったり下回ったりしますが、投資対象を分散することで、全体としてのリターンはある程度の水準に落ち着きます。
継続:市場の変動によって、リターンは大きく変動しますが、10年、20年と投資を継続することで、ある程度の水準に落ち着きます。
したがって、大数の法則を投資に当てはめると、以下のような考え方ができます。
「期待収益率の高い投資方針にしたがい、分散を心がけて投資を継続すれば、長期的には、偶然の要素に頼らずに、満足の行く投資結果を得られるだろう」
この考え方をすることができれば、投資家は、偶然の要素に頼ろうとしたり、市場の変動や個々の投資対象のリターンに惑わされて自身の投資方針を曲げたりすることなく、
○ 自身の投資方針の期待収益率を上げること
○ 結果を期待値に近付けること
に集中することができます。
この2つこそが、投資家が最もエネルギーを割くべき課題です。
まとめ
投資とはイチかバチかの勝負ではありません。何十年もの長期間に渡って資産を形成する行為なのです。
投資期間が長期間になればなるほど、偶然の要素は排除され、投資結果はその投資家が持つ本来の実力に近づいていきます。
偶然に頼らず、期待収益率を上げ、結果を期待値に近付ける努力をするのが、投資家のあるべき姿です。